Fórmula general
Consideremos la ecuación general de segundo grado (ecuación cuadrática) que tiene la forma:  .
.
Resolver esta ecuación implica encontrar el valor o los valores de que cumplen con la expresión, si es que existen.
que cumplen con la expresión, si es que existen.
Cuando nos enfrentamos por primera vez en la vida a esta clase de problemas, la primera forma en la que se intenta dar una respuesta es probando con varios números hasta "atinarle" (ya sea por que nos sonría la buena fortuna, o por aproximación).
Algunos incluso prueban número tras número hasta hallar la solución (Método de la "Fuerza Bruta").
Después, conforme nos vamos enfrentando a mas problemas que involucran ecuaciones cuadráticas, descubrimos algunos métodos de solución. De los primeros que aprendemos (por simplicidad) están el "Método Gráfico" (Realizar la gráfica correspondiente a la ecuación cuadrática igualada a cero y observar en que abscisas la gráfica "toca o pasa" por el eje horizontal del plano cartesiano). Otro método que aprendemos es el "Método de Factorización" (Trabajar con la expresión cuadrática igualada a cero hasta dejarla expresada como multiplicación de otras dos expresiones algebraicas, y encontrar "por simple observación" los valores que hacen que estas últimas dos ecuaciones sean iguales a cero).
Las desventajas de estos métodos es que implican trabajo excesivo, y no se garantiza que se encuentre la solución de la ecuación (al menos una solución "Real").
El último método que se estudia para resolver ecuaciones de segundo grado es la "Fórmula General".

Analizando la raíz cuadrada, se llega a las siguientes conclusiones:
 .
.Resolver esta ecuación implica encontrar el valor o los valores de
 que cumplen con la expresión, si es que existen.
que cumplen con la expresión, si es que existen.Cuando nos enfrentamos por primera vez en la vida a esta clase de problemas, la primera forma en la que se intenta dar una respuesta es probando con varios números hasta "atinarle" (ya sea por que nos sonría la buena fortuna, o por aproximación).
Algunos incluso prueban número tras número hasta hallar la solución (Método de la "Fuerza Bruta").
Después, conforme nos vamos enfrentando a mas problemas que involucran ecuaciones cuadráticas, descubrimos algunos métodos de solución. De los primeros que aprendemos (por simplicidad) están el "Método Gráfico" (Realizar la gráfica correspondiente a la ecuación cuadrática igualada a cero y observar en que abscisas la gráfica "toca o pasa" por el eje horizontal del plano cartesiano). Otro método que aprendemos es el "Método de Factorización" (Trabajar con la expresión cuadrática igualada a cero hasta dejarla expresada como multiplicación de otras dos expresiones algebraicas, y encontrar "por simple observación" los valores que hacen que estas últimas dos ecuaciones sean iguales a cero).
Las desventajas de estos métodos es que implican trabajo excesivo, y no se garantiza que se encuentre la solución de la ecuación (al menos una solución "Real").
El último método que se estudia para resolver ecuaciones de segundo grado es la "Fórmula General".

Analizando la raíz cuadrada, se llega a las siguientes conclusiones:
- Si
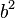 es menor que
es menor que  los resultados de X serán dos valores con parte real y parte imaginaria. Es decir, el resultado sera un número complejo.
los resultados de X serán dos valores con parte real y parte imaginaria. Es decir, el resultado sera un número complejo.
- Si
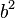 es mayor que
es mayor que  obtendremos dos valores distintos de X reales.
obtendremos dos valores distintos de X reales.
- Y si
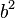 es igual que
es igual que  obtendremos dos valores de X reales e iguales.
obtendremos dos valores de X reales e iguales.
- Al término
 se le llama discriminante.
se le llama discriminante.

No hay comentarios:
Publicar un comentario