Binomio
En álgebra, un binomio consta únicamente de dos términos, separados por un signo de más (+) o de menos (-). En otras palabras, es una expresión algebraica formada por la suma o la resta de dos monomios.
Ejemplos
 .
. .
.
Operaciones sobre binomios
Factor común
Representación gráfica de la regla de factor común
El resultado de multiplicar un binomio a+b con un monomio c se obtiene aplicando la propiedad distributiva del producto respecto de la adición:
o realizando la operación:
Esta operación tiene una interpretación geométrica ilustrada en la figura. El área del rectángulo es c(a+b) (el producto de la base por la altura), pero también puede obtenerse como la suma de las dos áreas coloreadas (ca y cb).
Ejemplo:
Suma por diferencia
El binomio 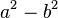 puede factorizarse como el producto de dos binomios:
puede factorizarse como el producto de dos binomios:
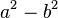 puede factorizarse como el producto de dos binomios:
puede factorizarse como el producto de dos binomios: .
.
Demostración:
Esta disposición suele llamarse diferencia de cuadrados, y es un caso especial de la fórmula:  .
.
 .
.
Producto de dos binomios lineales
El producto de un par de binomios lineales 
 es:
es:

 es:
es: .
.
Potencia de un binomio
Un binomio elevado a la n-ésima potencia, se escribe: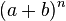 , y puede desarrollarse utilizando la fórmula de teorema de Newton o, equivalentemente, con ayuda del triángulo de Pascal. El ejemplo más sencillo es el cuadrado perfecto:
, y puede desarrollarse utilizando la fórmula de teorema de Newton o, equivalentemente, con ayuda del triángulo de Pascal. El ejemplo más sencillo es el cuadrado perfecto: 
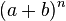 , y puede desarrollarse utilizando la fórmula de teorema de Newton o, equivalentemente, con ayuda del triángulo de Pascal. El ejemplo más sencillo es el cuadrado perfecto:
, y puede desarrollarse utilizando la fórmula de teorema de Newton o, equivalentemente, con ayuda del triángulo de Pascal. El ejemplo más sencillo es el cuadrado perfecto: 
Cuadrado de un binomio
Visualización de la fórmula para binomio al cuadrado
Al elevar un binomio al cuadrado, se lo multiplica por sí mismo:
.
La operación se efectúa del siguiente modo:
De aquí se puede derivar una regla para el cálculo directo: se suman
los cuadrados de cada término con el doble producto de los mismos.
Un trinomio de la forma  , se conoce como trinomio cuadrado perfecto;
, se conoce como trinomio cuadrado perfecto;
 , se conoce como trinomio cuadrado perfecto;
, se conoce como trinomio cuadrado perfecto;
Cuando el segundo término es negativo:
Ejemplo:








No hay comentarios:
Publicar un comentario