jueves, 26 de noviembre de 2015

Tabla de verdad

Una tabla de verdad, o tabla de valores de verdad, es una tabla que muestra el valor de verdad de una proposición compuesta, para cada combinación de verdad que se pueda asignar.

Verdadero

El valor verdadero se representa con la letra V; si se emplea notación numérica se expresa con un uno: 1; en un circuito eléctrico, el circuito está cerrado.

Falso

El valor falso se representa con la letra F; si se emplea notación numérica se expresa con un cero: 0; en un circuito eléctrico, el circuito está abierto.

Variable

Para una variable lógica A, B, C, ... que pueden ser verdaderas V, o falsas F, los operadores fundamentales se definen así:

\begin{array}{|c|c|} \hline A & A \\ \hline V & V \\ F & F \\ \hline \end{array}

Negación

La negación es un operador que se ejecuta, sobre un único valor de verdad, devolviendo el valor contradictorio de la proposición considerada.

\begin{array}{|c|c|} \hline A & \thicksim A \\ \hline V & F \\ F & V \\ \hline \end{array}

Conjunción

La conjunción es un operador que actúa sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de verdad verdadero cuando ambas proposiciones son verdaderas, y falso en cualquier otro caso. Es decir es verdadera cuando ambas son verdaderas
La tabla de verdad de la conjunción es la siguiente:

\begin{array}{|c|c|c|} \hline A & B & A \and B \\ \hline V & V & V \\ V & F & F \\ F & V & F \\ F & F & F \\ \hline \end{array}

Que se corresponde con la columna 8 del algoritmo fundamental.
en simbologia "^" hace referencia a el conector "y"

Disyunción

La disyunción es un operador que actúa sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de verdad verdadero cuando una de las proposiciones es verdadera, o cuando ambas lo son, y falso cuando ambas son falsas.
La tabla de verdad de la disyunción es la siguiente:

\begin{array}{|c|c|c|} \hline A & B & A \or B \\ \hline V & V & V \\ V & F & V \\ F & V & V \\ F & F & F \\ \hline \end{array}

Que se corresponde con la columna 2 del algoritmo fundamental.

Implicación o Condicional

El condicional material es un operador que actúa sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de falso sólo cuando la primera proposición es verdadera y la segunda falsa, y verdadero en cualquier otro caso.
La tabla de verdad del condicional material es la siguiente:

\begin{array}{|c|c|c|} \hline A & B & A \Rightarrow B \\ \hline V & V & V \\ V & F & F \\ F & V & V \\ F & F & V \\ \hline \end{array}

Que se corresponde con la columna 5 del algoritmo fundamental.

Equivalencia, doble implicación o Bicondicional

El bicondicional o doble implicación es un operador que funciona sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de verdad verdadero cuando ambas proposiciones tienen el mismo valor de verdad, y falso cuando sus valores de verdad son diferentes.
La tabla de verdad del bicondicional es la siguiente:

\begin{array}{|c|c|c|} \hline A & B & A \Leftrightarrow B \\ \hline V & V & V \\ V & F & F \\ F & V & F \\ F & F & V \\ \hline \end{array}

Que se corresponde con la columna 7 del algoritmo fundamental.

Número de combinaciones

Partiendo de un número n de variables, cada una de las cuales puede tomar el valor verdadero: V, o falso: F, por Combinatoria, podemos saber que el número total de combinaciones: Nc, que se pueden presentar es:

Nc = 2^n

el número de combinaciones que se pueden dar con n variable, cada una de las cuales puede tomar uno entre dos valores lógicos es de dos elevado a n, esto es, el número de combinaciones: Nc, tiene crecimiento exponencial respecto al número de variable n:

\begin{array}{r|r} n & Nc \\ \hline 0 & 1 \\ 1 & 2 \\ 2 & 4 \\ 3 & 8 \\ 4 & 16 \\ 5 & 32 \\ \ldots & \ldots \\ n & 2^n \end{array}

Si consideramos que un sistema combinacional de n variables binarias, puede presentar un resultado verdadero: V, o falso: F, para cada una de las posibles combinaciones de entrada tenemos que se pueden construir Cp circuitos posibles con n variables de entrada, donde:

Cp = 2^{2^{n}}

Que da como resultado la siguiente tabla:

\begin{array}{r|r} n & Cp\\ \hline 0 & 2 \\ 1 & 4 \\ 2 & 16 \\ 3 & 256 \\ 4 & 65_.536 \\ 5 & 4_.294.967.296 \\ \ldots & \ldots \\ n & 2^{2^{n}} \end{array}

Para componer una tabla de verdad, pondremos las n variables en una línea horizontal, debajo de estas variables desarrollamos las distintas combinaciones que se pueden formar con V y F, dando lugar a la distintas Nc, número de combinaciones. Normalmente solo se representa la función para la que se confecciona la tabla de verdad, y en todo caso funciones parciales que ayuden en su cálculo, en la figura, se pueden ver todas las combinaciones posibles Cp, que pueden darse para el número de variables dado.

Así podemos ver que para dos variables binarias: A y B, n= 2 , que pueden tomar los valores V y F, se pueden desarrollar cuatro combinaciones: Nc= 4, con estos valores se pueden definir dieciséis resultados distintos, Cp= 16, cada una de las cuales seria una función de dos variables binarias. Para otro número de variables se obtendrán los resultados correspondientes, dado el crecimiento exponencial de Nc, cuando n toma valores mayores de cuatro o cinco, la representación en un cuadro resulta compleja, y si se quiere representar las combinaciones posibles Cp, resulta ya complejo para n= 3.

EJEMPLOS DE DIAGRAMAS

DIAGRAMA DE FLUJO- La presentación gráfica desistemas.- Permite identificar aspectosrelevantes de una manerarápida y si...

DEFINICIÓN Es una técnica que permite representar gráficamente las operaciones y estructuras que se van a realiza...

Diagramas de flujo

Un diagrama de flujo es una representación gráfica de un proceso. Cada paso del proceso es representado por un símbolo diferente que contiene una breve descripción de la etapa de proceso. Los símbolos gráficos del flujo del proceso están unidos entre sí con flechas que indican la dirección de flujo del proceso.

El diagrama de flujo ofrece una descripción visual de las actividades implicadas en un proceso mostrando la relación secuencial ente ellas, facilitando la rápida comprensión de cada actividad y su relación con las demás, el flujo de la información y los materiales, las ramas en el proceso, la existencia de bucles repetitivos, el número de pasos del proceso, las operaciones de interdepartamentales… Facilita también la selección de indicadores de proceso.

Elaboración del Diagrama de Flujo

El diagrama de flujo debe ser realizado por un equipo de trabajo en el que las distintas personas aporten, en conjunto, una perspectiva completa del proceso, por lo que con frecuencia este equipo será multifuncional y multijerárquico.

Determinar el proceso a diagramar.
Definir el grado de detalle. El diagrama de flujo del proceso puede mostrar a grandes rasgos la información sobre el flujo general de actividades pricipales, o ser desarrollado de modo que se incluyan todas las actividades y los puntos de decisión. Un diagrama de flujo detallado dará la oportunidad de llevar realizar un análisis más exhaustivo del proceso.
Identificar la secuencia de pasos del proceso. Situándolos en el orden en que son llevados a cabo.
Construir el diagrama de flujo.

Circuitos de Euler

CIRCUITO DE EULER

En la teoría de grafos , un camino euleriano es un camino en un gráfico que visita cada borde exactamente una vez. Del mismo modo, un circuito euleriano o ciclo euleriano es un camino euleriano que comienza y termina en el mismo vértice. Euler demostró que una condición necesaria para la existencia de circuitos de Euler es que todos los vértices de la gráfica tiene una aún grado , y afirmó sin pruebas que los gráficos relacionados con todos los vértices de grado par tiene un circuito euleriano.

Euler demostró que es sencillo determinar si existe un camino de Euler en el grafo, ya que todo lo que hay que hacer es verificar el grado de los nodos. Existen un teorema de la teoría de grafos que establece que un grafo tiene un camino de Euler si y solo sí es este es conexo y exactamente dos de sus nodos tienen grado impar. De manera similar, un grafo tiene un tour de Euler si y solo sí es conexo y todos sus nodos tienen grado par.

Basado en estos teoremas se puede verificar la existencia de un camino de Euler antes de intentar encontrar el camino, lo cual podría ahorrar una gran cantidad de procesamiento en la búsqueda de un camino que nunca logrará encontrarse. Además, la comprobación de grado de los nodos de un grafo es una tarea que fácilmente podría ser de complejidad lineal en el número de nodos del mismo.

Una técnica más adecuada es la de encontrar ciclos en el grafo, borrando de las listas de adyacencia las aristas que se encuentren y almacenando en un pila los nodos que se vayan encontrando, de tal manera de registrar los nodos del camino e imprimir sus enlaces, así como poder verificar caminos alternativos en cada nodo. Esta técnica puede encontrar un tour de Euler, si existe en el grafo, en tiempo lineal.

El siguiente ejemplo ilustra el funcionamiento de esta estrategia sobre un grafo de ejemplo. La secuencia de ilustraciones va de izquierda a derecha y de arriba hacia abajo. En cada una de las figuras podemos ver el grafo, las lista de adyacencia de cada nodo y la pila P que lleva registro del tour. El tour comienza en el nodo 0 y la primera arista a visitar es la 0-1. Nótemos que en la primera figura P dicha arista no aparece en las listas y que en P ya se encuentran los nodos 0 y 1.

Una vez que las listas de adyacencias estén vacías el algoritmo ha culminado su ejecución. La secuencia de nodos que se desapilan de P nos indican un tour de Euler posible para el grafo anterior: 0-6-4-3-2-4-5-0-2-1-0.

Ahora bien, supóngamos que en la sexta imagen no se hubiese viajado al nodo 2 sino al nodo 6, entonces en la séptima figura se hubiese viajado al nodo 0 y desde este último no podemos elegir más enlaces, lo mismo ocurre con el nodo 6. En estos casos el algoritmo desapila de P los nodos aislados y continua con el nodo 4, en cuyo caso el algoritmo culminaría cuando P contenga los identificadores: 0 1 2 0 5 4 3 2 4. Es evidente que desde 4 se puede alcanzar a 6 y a 0 porque estaban apilados luego de él en la pila, así que basta con apilarlos de nuevo en el orden en que apilados originalmente: 6 0. En esta variante del problema se obtendría un tour de Euler diferente al anterior: 0-6-4-2-3-4-5-0-2-1-0.

Grafo

Grafo

Un grafo en el ámbito de las ciencias de la computación es una estructura de datos, en concreto un tipo abstracto de datos (TAD), que consiste en un conjunto de nodos (también llamados vértices) y un conjunto de arcos (aristas) que establecen relaciones entre los nodos. El concepto de grafo TAD desciende directamente del concepto matemático de grafo.

La teoría de grafos (también llamada teoría de las gráficas) es un campo de estudio de las matemáticas y las ciencias de la computación, que estudia las propiedades de los grafos (también llamadas gráficas, que no se debe confundir con las gráficas que tienen una acepción muy amplia) estructuras que constan de dos partes, el conjunto de vértices, nodos o puntos; y el conjunto de aristas, líneas o lados que pueden ser orientados o no. Por ello, también se conoce como análisis de redes.

http://blogs.ua.es/matematicadiscrecion/files/2011/01/Caminosmascortos.jpg

BINOMIOS

Binomio

Para otros usos de este término, véase binomial (desambiguación).

En álgebra, un binomio consta únicamente de dos términos, separados por un signo de más (+) o de menos (-). En otras palabras, es una expresión algebraica formada por la suma o la resta de dos monomios.

Ejemplos

$a+b$ .
$a^2b^5c^2d-b^3c^9d^2$ .

Operaciones sobre binomios

Factor común

Representación gráfica de la regla de factor común

El resultado de multiplicar un binomio a+b con un monomio c se obtiene aplicando la propiedad distributiva del producto respecto de la adición:

$c (a + b) = c a + c b$

o realizando la operación:

$\begin{array}{rrr} & a & +b \\ \times & & c \\ \hline & ca & +cb \end{array}$

Esta operación tiene una interpretación geométrica ilustrada en la figura. El área del rectángulo es c(a+b) (el producto de la base por la altura), pero también puede obtenerse como la suma de las dos áreas coloreadas (ca y cb).

Ejemplo:

3x (4x-6y) = (3x)(4x) + (3x)(-6y) = 12x^2 - 18xy

Suma por diferencia

El binomio

a^2 - b^2

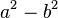puede factorizarse como el producto de dos binomios:

a^2 - b^2 = (a + b)(a - b)

Demostración:

\begin{array}{rrr} & a & +b \\ \times & a & -b \\ \hline & -ab & -b^2 \\ a^2 & +ab & \\ \hline a^2 & & -b^2 \end{array}

Esta disposición suele llamarse diferencia de cuadrados, y es un caso especial de la fórmula:

a^{n+1} - b^{n+1} = (a - b)\sum_{k=0}^{n} a^{k}\,b^{n-k}

Producto de dos binomios lineales

El producto de un par de binomios lineales

(ax+b)

(cx+d)

es:

(ax+b)(cx+d) = acx^2 + axd + bcx + bd = acx^2 + (ad + bc)x + bd

Potencia de un binomio

Un binomio elevado a la n-ésima potencia, se escribe:

(a + b)^n

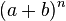, y puede desarrollarse utilizando la fórmula de teorema de Newton o, equivalentemente, con ayuda del triángulo de Pascal. El ejemplo más sencillo es el cuadrado perfecto:

(p+q)^2

Cuadrado de un binomio

Visualización de la fórmula para binomio al cuadrado

Al elevar un binomio al cuadrado, se lo multiplica por sí mismo:

$(a + b)^2 = (a + b) (a + b) = a^2 + 2 a b + b^2$ .

La operación se efectúa del siguiente modo:

$\begin{array}{rrr} & a & +b \\ \times & a & +b \\ \hline & +ab & +b^2 \\ a^2 & +ab & \\ \hline a^2 & +2ab & +b^2 \end{array}$

De aquí se puede derivar una regla para el cálculo directo: se suman los cuadrados de cada término con el doble producto de los mismos.

Un trinomio de la forma

a^2 + 2 a b + b^2

, se conoce como trinomio cuadrado perfecto;

Cuando el segundo término es negativo:

$(a - b)^2 = (a - b) (a - b) = a^2 - 2 a b + b^2$

$\begin{array}{rrr} & a & -b \\ \times & a & -b \\ \hline & -ab & +b^2 \\ a^2 & -ab & \\ \hline a^2 & -2ab & +b^2 \end{array}$

Ejemplo:

(2x - 3y)^2 = (2x)^2 + 2(2x)(-3y)+ (-3y)^2 = 4x^2 -12xy +9y^2

SUSTITUCION DE DATOS

Graficando con Puntos

Una función cuadrática es un polinomio de grado 2, es decir, el exponente más alto en la variable es 2. Los siguientes son ejemplos de funciones cuadráticas:

La función cuadrática más básica y simple tiene la ecuación

. Si hacemos una tabla con los valores de esta función, vemos que el rango (los valores de y, o salida) no se comportan como una función lineal. En una función lineal, el valor de y cambia por la misma cantidad cada vez que el valor de x aumenta por 1. Eso no sucede con una función cuadrática:

x	y = x²
-3	9
-2	4
-1	1
0	0
1	1
2	4
3	9

Los valores de y no cambian por una cantidad constante. Grafiquemos algunos puntos para ver cómo se vería la función:

Después de graficar algunos puntos, podría ser tentador conectar los puntos con segmentos de línea, que son rectos. Pero esto estaría mal, y produciría un patrón que no representa la función.

Borremos esas líneas rectas y grafiquemos el resto de los puntos:

Ahora dibujamos una curva suave conectando los puntos.

¡Mejor! Una función cuadrática resulta en una gráfica con forma de U, llamada parábola. Los valores de la función cambian suavemente, por lo que la curva debe ser suave también. Ahora que podemos ver la naturaleza de la parábola (forma de U), veamos su forma en detalle.

Características de una Parábola

La forma estándar de una ecuación cuadrática es

. Por ejemplo

, el valor del coeficiente a es 1, y b y c son 0. Si bien muchas ecuaciones cuadráticas presentan valores de b y c diferentes de cero, la gráfica resultante siempre será una parábola.

Las parábolas tienen muchas propiedades que pueden ayudarnos a graficar ecuaciones cuadráticas. Una parábola tiene un punto especial llamado vértice; este es el punto donde la U "da la vuelta". Nota que en el vértice, la parábola cambia de dirección:

El vértice es el punto más alto o más bajo de la curva, dependiendo si la U se abre hacia arriba o hacia abajo. En el caso de que la parábola abra hacia arriba, el vértice será su punto más bajo; y una parábola que abre hacia abajo, tendrá un vértice en su punto más alto.